The Python code available on this page is a collection of classes and support functions for visualizing inversive and hyperbolic geometry, with the hyperbolic examples utilizing the Poincaré disc model. For more online information on hyperbolic geometry see here.
I was prompted to develop this software while reading about these topics in the excellent textbook "Geometry" by David A. Brannan, Matthew F. Esplen, and Jeremy J. Gray, Cambridge University Press; 2nd ed., and in particular chapters 5 and 6. I also found chapter 10 of "Euclidean and Non-Euclidean Geometries" by Marvin J. Greenberg, W.H. Freeman, 4th ed., useful for additional information on hyperbolic trigonometry.
I've 'repurposed' most of my code from two sources – Casey Duckering's Python hyperbolic library and the hyperbolic_tessellation code in Section 16.7 of "A Programmer's Introduction to Mathematics" by Jeremy Kun. My main 'contribution', especially in the case of Duckering library, was to drastically simplify the implementation. The difference can be seen by comparing the output of one of his examples with a similar version using my library:

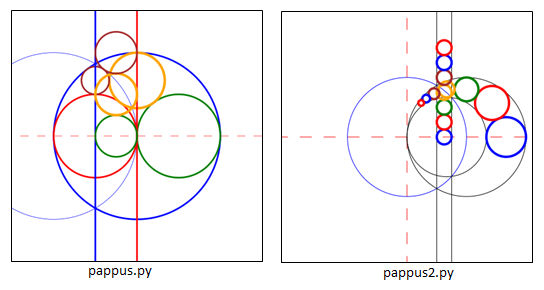
The difference reflects one of my aims: to make the code simple enough to be easily understood while still being able to reproduce most of the drawings in chapters 5 and 6 of Brannan et al.. Also, in the context of inversion geometry, I wanted to generate a Pappus Chain similar to one drawn by hand in the Numberphile Youtube video "Epic Circles". My results are shown below:
A central aim of my hyperbolic geometry code, and the reason for using the Poncaré Disk Model, was to generate versions of M.C. Escher's four Circle Limit drawings:

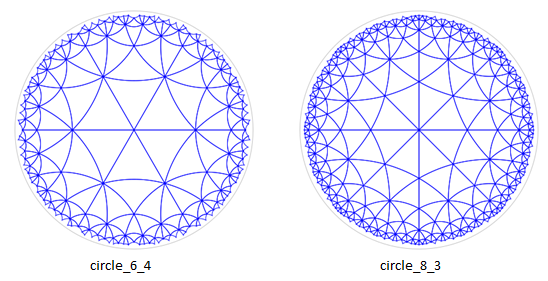
The hyperbolic plane can be tessellated using p-sided polygons with q of them meeting at each vertex provided that (p-2)(q-2) > 4, which can be denoted as {p,q}. Escher used the regular tessellations {6,4} for Circle Limit I and IV, and {8,3} for Circle Limit II and III.
My Circle Limit code (circleLimit.py) generates the following images when supplied with the necessary values for p and q:
As these examples show, my library only supports right-angled hyperbolic triangles, not arbitrary images, or even regular polygons. However, it is fairly simple to build polygons by reflecting triangles around specific edges.
My triangles can also be understood as right-angled hyperbolic Schwarz triangles, commonly denoted by {p, q, r}, with vertex angles π/p, π/q, and π/r. In my case, one of these angles, for instance at r, is always π/2, so its value is always 2.
It's worth noting that Escher's Circle Limit III is a little more complicated than the others. The backbone arcs of the fish are not quite hyperbolic lines, touching the bounding circle at an angle of about 80° rather than 90°. Also, Douglas Dunham employs a triplet notation to capture how the fish meet at a vertex, since four meet at right fin tips, three meet at left fin tips, and three fish meet at their noses. Dunham's website is a gold mine of interesting papers on hyperbolic geometry and Escher
My Python code relies on three modules: numpy (for a tiny amount of linear algebra), matplotlib (for displaying the drawings), and drawsvg (for rendering the drawings as SVGs, although the final output is in PNG format). drawsvg is by Casey Duckering, the same developer as the Python hyperbolic library mentioned above.
The inversion geometry classes and utilities are in geom.py. The classes are ELine, EVertical, ESegment, ECircle, and EArc ("E" stands for Euclidean). The utilities roughly divide into groups related to intersection-finding, and extras for simplifying the use of matplotlib and drawsvg.
The hyperbolic geometry classes and utilities are in pgeom.py ("p" stands for Poincaré disk model). The classes are Point, Ideal, Line, Triangle, Circle, and Transform. The Transform class implements several Möbius transformations, including translation, rotation, complex conjugation, matrix inversion, and mirroring.
The geom.py and pgeom.py features are illustrated through many short examples, which are listed in readme.txt in the zip file. Every Python example generates a correspondingly named PNG file, which I've also included in the zip.
Two fun inversion examples are invParabola.py and invTangents.py whose outputs are:
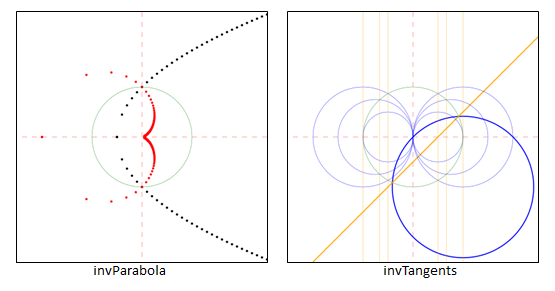
invParabola.py inverts sample points from a parabola, creating the coordinates of a cardioid. invTangents.py inverts several blue circles that all have a tangent to the y-axis. The thick blue circle which passes through the origin intersects all of these circles at the same angle, which is apparent by looking at how its inverse (an orange line) intersects their inverted lines. This example comes from Fig. 29 in chapter 4 of "Excursions in Geometry" by C.S. Ogilvy, Dover, 1990.
The hyperbolic geometry examples fall into three main groups:
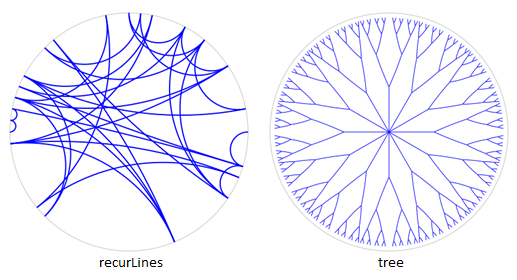
Two pretty hyperbolic examples are recurLines.py and tree.py whose outputs are: